Water wall...
Thermal Mass
A material’s capacity to absorb, store and release heat. Thermal mass is typically used to moderate temperature extremes by releasing heat when the home is cool and absorbing heat when the home is warm.
Specific heat capacity
A material's capacity to store heat (measured per unit mass). Some materials are better at storing heat than others. Water can store 4× as much heat per kilogram as concrete.
Density
Mass per unit volume (mass / volume). Denser materials have more mass per volume so they can make up in density what they lack in specific heat capacity. Concrete has twice as much mass per m3 as water.
Thermal conductivity
The ease with which heat travels through a material. Ideally, thermal conductivity should be moderate so that the absorption and release of heat synchronises with the building's heating and cooling cycle. Both water and concrete are highly effective! In comparison, steel and water hold a similar amount of heat per volume, but the steel heats and cools too quickly to be good thermal mass.
Effective thickness
Only the first ~ 50mm of concrete store / release heat on a daily timescale. Water is a liquid (and these water tubes are relatively small) so the entire water volume acts as thermal mass.
Our water wall:
- Ten tubes with an average diameter of 0.32m. Filled to 2.4m
- 0.194 m3 (or 194 L) water × 10 tubes × 1000 kg / m3 = 1940 kg water
- 1940 kg × 4.2 kJ × 1 °C / 3600 = 2.2 kWh per degree Celsius
Concrete required to match that thermal mass:
- 2.2kWh = 8148 kg concrete × 1.0 kJ × 1 °C / 3600
- 8148 kg / 2000 kg/m3 = 4.1 m3 or 82m2 as a 50mm thick layer.
Actual data?
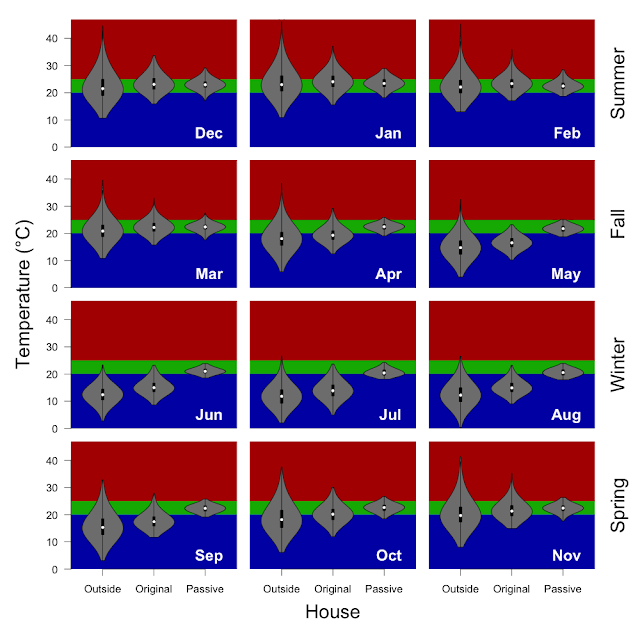
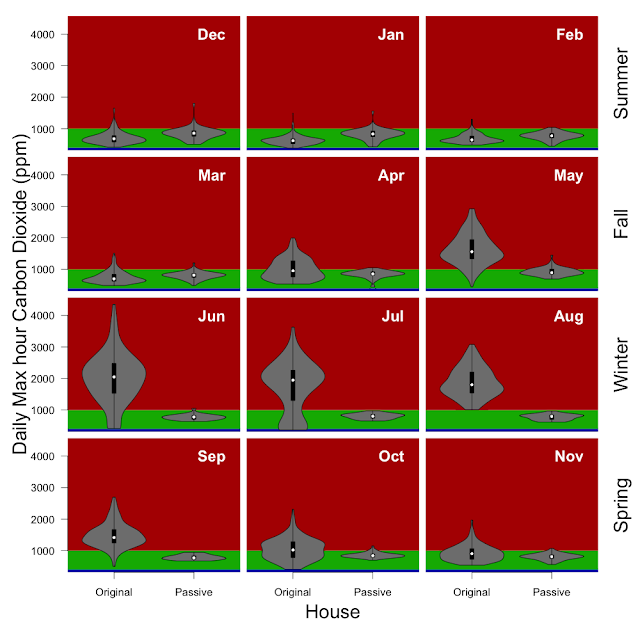
I am open to suggestions on the best way to calculate these things, but here is attempt 1. In an effort to get an idea about how much heat is being stored during the day at released at night - I took the hourly median temperature from 6am and 6pm as indicative of the temperature at dawn and dusk (yeah, can do it more precisely but this is the first go at it). Two of the water tubes have temperature sensors, and I'll assume that they are reflective of all ten tubes. There is an air temperature sensor right next to the tubes as well as one in the kitchen which is at the opposite end of the house, but still in the same room.
- Kitchen: the typical (median) daily swing is 2.6 °C.
- Water wall air sensor: the median swing is 1.5 °C.
- The water in the tubes: the median swing is 0.6 °C.
Going back to the math above (2.2kW per °C) means that the tubes are effectively absorbing ~ 1.3kW of heat during the day which is released at night.
Not quite what we want
What we really want to know is how that works when it matters... say winter versus summer:
- Water tubes: 0.85 °C in winter vs. 0.52 °C in summer.
- Water wall air: 1.6 °C in winter vs. 1.4 °C in summer.
- Kitchen: 2.7 °C in winter vs. 2.3 °C in summer.
It is important to note that it is a zero sum game... heat absorbed must be released, and for the most part the timescale of the energy exchange is daily. While the Kitchen and even the air temperature near the water wall is bimodal with two distinct peaks even on an annual scale, the water tubes themselves do not have a bimodal temperature distribution at an annual scale. This is because the daily range (less than 1 °C) is less than the seasonal range. With a season a bimodal distribution is observed.